Sensori

08/12/2007

Autore: Leda Masi

Lunghezza focale, angolo di campo e fattore di moltiplicazione digitale.

La lunghezza focale, con annessi e implicazioni, è uno dei tormentoni della fotografia digitale, fonte di infinite discussioni.

Quello che segue è un compendio delle informazioni sulla lunghezza focale (e le sue conseguenze) che si trovano numerose, ma sparse, in rete e sui libri. Ho cercato di riunirle in un discorso il più possibile organico, perché possa essere uno strumento utile in questo campo, un po’ confuso, della fotografia digitale.
Cominciamo con una definizione ed una premessa.

Definizione: la lunghezza focale è la distanza fra il centro ottico dell’obiettivo ed il piano dell’elemento sensibile (pellicola o sensore)*vd nota 1. Questo valore è una caratteristica invariabile di ciascun obiettivo, qualunque sia la fotocamera su cui esso è montato. Tornerò più avanti su questo argomento.

Nota 1. Esistono particolari accorgimenti per ottenere che il centro ottico dell’obiettivo non si trovi nel centro fisico, ma spostato lungo l’asse, a volte fino ad essere esterno all’obiettivo stesso. Questo serve, ad esempio, a realizzare obiettivi per reflex con focali molto corte ma che possano essere montati sull’innesto standard senza prolungarsi entro la macchina, dove bloccherebbero il movimento dello specchietto.

Premessa: l’angolo di campo di un obiettivo dipende sia dalla sua lunghezza focale che dalle dimensioni dell’elemento sensibile.
Attenzione! Le variabili sono due ed in conseguenza non esistono focali “lungheï¿½ï¿½? o “corteï¿½ï¿½? in modo assoluto, ma solo in rapporto alla dimensione dell’elemento sensibile.

All’aumentare della lunghezza focale dell’obiettivo si riduce il suo angolo di campo, cioè l’ampiezza della scena ripresa. Così, a parità di formato del supporto, obiettivi con focali corte hanno una copertura maggiore di obiettivi con focali più lunghe.
Questo influisce naturalmente sulla foto finale, e obiettivi diversi vengono utilizzati per ottenere effetti e tagli diversi. Normalmente un obiettivo di focale “cortaï¿½ï¿½? viene impiegato per fotografare oggetti vicini oppure per abbracciare un’ampia porzione di spazio, mentre obiettivi “più lunghiï¿½ï¿½? vengono utilizzati per avvicinare soggetti distanti oppure per isolare un soggetto dal contesto.

Quanto detto vale qualunque sia il supporto di memorizzazione, o elemento sensibile che dir si voglia. Il problema è che le fotocamere reflex a pellicola ci hanno abituato a considerare “standardï¿½ï¿½? un formato dell’elemento sensibile di 24*36 mm, mentre le digitali montano sensori che hanno dimensioni estremamente variabili, da 4 – 5 mm fino a 24*36 (i cosiddetti full frame) e addirittura più grandi (dorsi per medio o grande formato).

Che cosa succede quando varia la dimensione del supporto?
Succede che gli obiettivi cambiano il loro angolo di campo: a parità di distanza e di lunghezza focale, al diminuire della dimensione del sensore l’angolo di campo diminuisce (in altre parole è come se la lunghezza focale aumentasse), mentre supporti più grandi del 24*36 causano un allargamento dell’angolo di campo (come se la focale divenisse più corta).

Vediamo perché questo avviene.
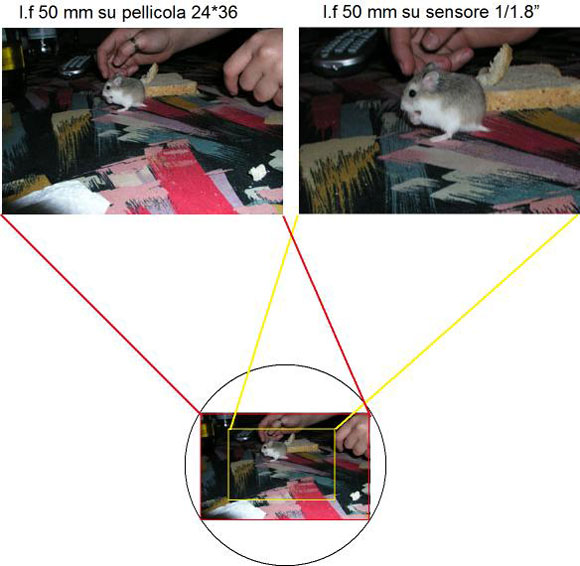
Un obiettivo produce un’immagine circolare che viene proiettata sul supporto, normalmente rettangolare. Quindi sul supporto rimane impressa la parte rettangolare che sta all’interno di questo cerchio. I normali obiettivi in commercio producono dei cerchi immagine che hanno un diametro pari alla diagonale del fotogramma 24*36, circa 43,3 mm. Quindi, su una fotocamera 35 mm l’immagine fissata sulla pellicola corrisponde alla parte centrale del cerchio e la diagonale dell’immagine corrisponde al diametro.
Se lo stesso obiettivo proiettasse l’immagine su di un sensore più grande (ad esempio su di una pellicola di medio formato), riuscirebbe a coprire solo la parte centrale (ricordiamo che la distanza fra obiettivo e piano sensibile è fissa e dipende solo dalla lunghezza focale).
Se invece l’immagine circolare viene proiettata su un sensore di dimensioni più piccole, la diagonale dell’immagine non corrisponde più al diametro dell’immagine proiettata, ma solo alla sua parte centrale, corrispondente alla diagonale del sensore.
Questo fenomeno si traduce in un “avvicinamentoï¿½ï¿½? e “ingrandimentoï¿½ï¿½? dell’immagine fotografata; è come se l’obiettivo avesse cambiato lunghezza focale, allungandosi, e di conseguenza avesse ridotto il suo angolo di campo, oppure come se avessimo utilizzato un moltiplicatore di focale.

Come si può vedere dal disegno, su un sensore più piccolo della pellicola (in giallo) l’immagine ripresa corrisponde a una parte di quella ripresa con un 24*36, e l’effetto è quello di un medio tele.
L’obiettivo in realtà ha inquadrato la stessa porzione di spazio, mantiene cioè le sue proprietà ottiche, quello che varia è la porzione di spazio effettivamente impressa sul supporto.

La differenza di angolo di copertura si traduce nel cosiddetto Fattore di Moltiplicazione Digitale .
Questo è una costante che si ottiene dividendo la diagonale del fotogramma 24*36 per la diagonale del sensore in uso [43,3/d]. Si indica con (N)x ed è quel numero per il quale bisogna moltiplicare la lunghezza focale usata, per conoscere a quale lunghezza focale equivarrebbe sul formato 35 mm, o per sapere quale lunghezza focale utilizzare per ottenere la stessa copertura di un determinato obiettivo sul 35 mm.

Tanto per dare un minimo di concretezza al discorso, vediamo le dimensioni dei principali sensori in commercio e i loro fattori di moltiplicazione:

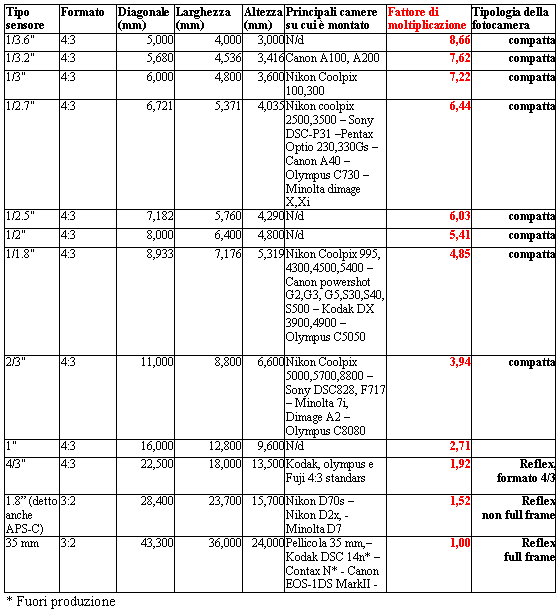
Due osservazioni saltano agli occhi.
La prima è che tutte le compatte hanno dei fattori di moltiplicazione “importantiï¿½ï¿½?, che partono da 4 per arrivare a oltre 7. A tutti gli effetti queste fotocamere sono una categoria a sé e per ciascuna di esse le case, abitualmente, si preoccupano di specificare anche la “lunghezza focale equivalenteï¿½ï¿½? (la vedremo alla prossima tabella).
La seconda è che solo una reflex (la Canon 1DS MKII) ha un sensore full frame: tutte le altre reflex Canon e di tutte altre case (ad oggi Pentax – Samsung, Sony – Minolta, Nikon, Fuji, Sigma) hanno sensori più piccoli, genericamente definiti APS size. Queste dimensioni non sono standardizzate (a volte nemmeno pubblicate), ma si piazzano intorno ad in fattore di moltiplicazione che sta fra 1,3 e 1,6.
Fanno categoria a sé le reflex del sistema 4/3 (ad oggi Olympus e Panasonic), il cui sensore ha un fattore di moltiplicazione di circa 2 (questo facilita i calcoli).

Come si può facilmente intuire, più piccolo il sensore e maggiore sarà l’effetto di “allungamentoï¿½ï¿½? della lunghezza focale.

Vediamo un’altra tavola: vi sono elencate le lunghezze focali principali rapportate ai diversi formati di sensore. Ad ogni lunghezza focale reale corrispondono diverse lunghezze focali “apparentiï¿½ï¿½? dovute al fattore di moltiplicazione dei diversi sensori.

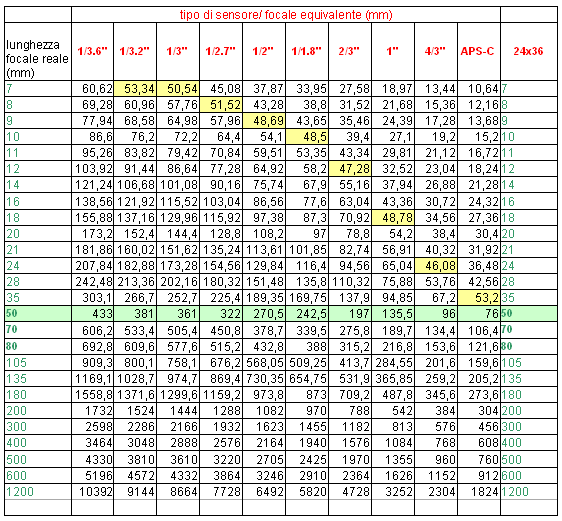
Ho evidenziato in verde l’obiettivo “normaleï¿½ï¿½?, il 50 mm, per mettere in rilievo come cambi radicalmente in funzione delle dimensioni del sensore: come si vede facilmente da obiettivo “normaleï¿½ï¿½? su una 35 mm diventa un tele già nel formato 4/3 per trasformarsi in un potentissimo tele se le dimensioni del sensore si riducono ulteriormente. In giallo ho invece evidenziato per i differenti formati quale dovrebbe essere la lunghezza focale da usare per ottenere un obiettivo “normaleï¿½ï¿½?; come si vede per avere la copertura di un 50 mm con un sensore 1/1.8ï¿½ï¿½? (quello usato per l’illustrazione sopra) dovrei usare un 10 mm. (cosa che ho effettivamente fatto, ma ne parliamo più avanti). È evidente che lo scostamento di lunghezza focale richiesta si riduce mano a mano che le dimensioni del sensore si avvicinano a quelle del fotogramma: così su un APS-C (1.8ï¿½ï¿½?) devo usare un 35 mm per ottenere (circa) la copertura di un 50 mm, mentre dovrò usare un 10 mm se le dimensioni del sensore scendono al 1/1,8ï¿½ï¿½?.

Gli effetti descritti si applicano a tutti gli obiettivi: nel caso di reflex saprò già che obiettivo sto utilizzando e quindi è semplice trovare a quale angolo di copertura (o “focale equivalenteï¿½ï¿½?) in realtà corrisponde a seconda del sensore. Usando una compatta digitale, normalmente dotate di obiettivo zoom, nel caso servisse sapere la “focale equivalenteï¿½ï¿½? utilizzata, basta guardare nei dati exif della foto, e poi moltiplicare il valore della focale utilizzata per il fattore di moltiplicazione per conoscere a quale lunghezza focale corrisponderebbe su un 35 mm.

Vediamo adesso una tabella che mette in relazione le lunghezze focali, per un formato 35 mm, con gli angoli di copertura dei diversi obiettivi.
Il dato è interessante in quanto tiene conto sia della lunghezza focale che della dimensione del sensore. In conseguenza l’angolo di copertura può finalmente indicare un “valore assolutoï¿½ï¿½? rispetto alla scena ripresa. Un obiettivo con un angolo di copertura di 46° sarà sempre un obiettivo “normaleï¿½ï¿½?, quali che siano lunghezza focali e dimensioni del sensore. Che naturalmente dovranno stare fra loro in un rapporto ben determinato, ma questo lo abbiamo già detto e sarà mostrato in dettaglio più sotto.
Ribadisco che è l’angolo di copertura – e solo quello – a determinare se un obiettivo sarà normale, tele o grandangolare.

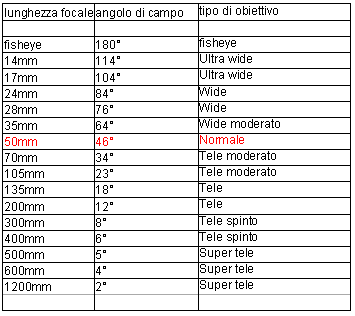
Le classificazioni nella colonna di destra hanno un valore indicativo, servono per capirsi. Non so se esista una Tabella Ufficiale che prescriva una terminologia unificata.

Come già detto, variando le dimensioni del supporto di memorizzazione delle immagini cambia la copertura dell’obiettivo.Per chi vuole scendere nei dettagli, nello schema seguente sono riportati gli angoli di campo dei differenti obiettivi per i più comuni sensori.

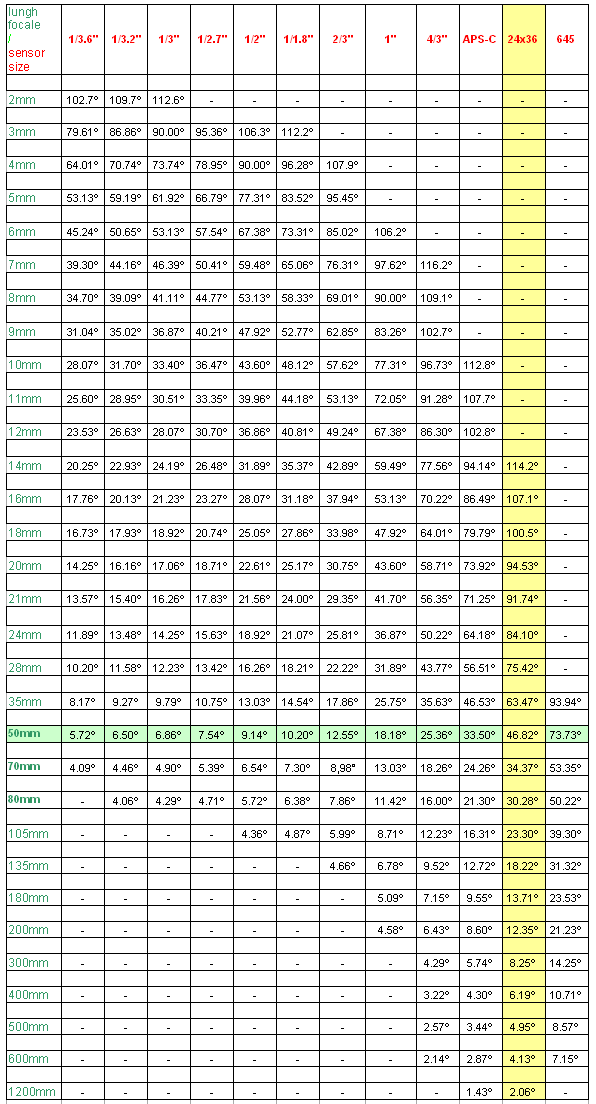
nota: la formula per calcolare l’angolo di campo effettivamente coperto da una certa lunghezza focale su un dato sensore è: α=2*arctan(d/2f) dove d è la diagonale del sensore e f la focale reale. Giusto per chi si ricorda ancora la trigonometria e volesse calcolarsi altre lunghezze focali che non trova qui riportate.
Sono debitrice per questa tabella a Emanuele A. “Juzaï¿½ï¿½? ( www.juzaphoto.com ) che gentilmente mi ha concesso di utilizzare la tabella che faticosamente aveva calcolato, permettendomi così di non dover rifare tutti i calcoli. La tabella e l’articolo relativo sono pubblicati su www.photorevolt.com ottimo sito di fotografia cui Emanuele collabora assiduamente.

Anche qui ho evidenziato la variazione della copertura di un 50 mm relativamente ai diversi formati di sensore e le coperture delle diverse ottiche sul formato 24*36.

Da questo effetto di moltiplicazione della focale discendono benefici e problemi, com’è facile intuire.
Un primo grande problema riguarda gli obiettivi grandangolari: per avere angoli di campo sufficientemente ampi, come quelli che avremmo ad esempio con un 28 mm, su un sensore più piccolo (diciamo con un fattore di moltiplicazione di 1,6x, dovremmo utilizzare un obiettivo di lunghezza focale 17 mm (cioè un fortissimo grandangolo).

D’altro canto, i teleobiettivi aumentano il loro potere di ingrandimento, come se diventassero più lunghi, o come se si utilizzasse un moltiplicatore di focale. Mantenendo però, e qui sta il bello, la medesima luminosità dell’obiettivo reale.

Sappiamo infatti che la luminosità di un obiettivo è funzione del suo diametro e della sua lunghezza (lunghezza focale diviso diametro); per effetto del fattore di moltiplicazione cambia l’angolo di campo (come se la lunghezza focale aumentasse) ma il diametro e la lunghezza “fisicaï¿½ï¿½? dell’obiettivo non variano, quindi non varia il loro rapporto; di conseguenza non cambia la luminosità. Un obiettivo da 200 mm diventa un 300 mm su un sensore con un fattore 1,5x. Un obiettivo 200 mm f/2,8 ha un peso e un costo, un obiettivo 300 mm f/2,8 ha ben altro peso e ben altro costo! Utilizzando il mio 200 mm f/2,8 su un tale sensore ho l’effetto di magnificazione senza perdere la luminosità e con un bel risparmio in termini di denaro e di peso. Mica male, no?
Lo stesso discorso riguarda i moltiplicatori di focale: questi ultimi sono tubi aggiuntivi che “allunganoï¿½ï¿½? l’obiettivo, ottenendo lo stesso effetto di magnificazione, ma l’allungamento è fisico, reale, e quindi incide anche sulla luminosità dell’obiettivo. Usando lo stesso obiettivo su una reflex digitale, ottengo lo stesso risultato dell’uso di un moltiplicatore, ma senza la relativa perdita di luminosità.
Negli obiettivi reflex “disegnati per il digitaleï¿½ï¿½? – ossia per coprire sensori più piccoli di 24*36 – è possibile usare lenti più piccole, a parità di luminosità, o avere una luminosità maggiore senza aumentare dimensioni, peso e costo.
In generale la spinta verso sensori più piccoli, anche nelle reflex, deriva dalla possibilità di costruire lenti più leggere e/o luminose a parità di costo. Resta il problema della risoluzione, che i sensori digitali mettono severamente alla prova, ma le lenti odierne sono in grado di cavarsela adeguatamente.

Un’altra importante differenza riguarda la profondità di campo.
Sappiamo già che la profondità di campo è funzione, fra le altre cose, della lunghezza focale.
All’aumentare della lunghezza focale diminuisce la profondità di campo, fino a ridursi a pochi mm per i teleobiettivi più spinti. Un obiettivo creato per il 35 mm e utilizzato su una digitale con sensore più piccolo, darà quindi lo stesso angolo di campo di un obiettivo di focale più lunga, ma la medesima profondità di campo di quello originale, dal momento che la lunghezza dell’obiettivo è un dato fisico, oggettivo e immutabile.
Per fare un esempio, con il 200 mm di cui sopra ho la copertura e l’effetto ingrandimento del 300, ma con la profondità di campo offerta dal 200.

Tutto ciò vale se parliamo di reflex digitali accoppiate a obiettivi per il 35 mm, che generano quindi un cerchio immagine di dimensioni adeguate al fotogramma.
Le lenti montate sulle compatte hanno invece generalmente lunghezze focali molto, molto corte, per dare angoli di campo accettabili e sono progettate per creare cerchi immagine più piccoli, adeguati alle piccole dimensioni dei sensori. Sono quindi molto più piccoli e leggeri, e a causa della loro ridotta lunghezza focale danno una profondità di campo maggiore di quella che si avrebbe su focali equivalenti.
Questo effetto di aumento della profondità di campo è parzialmente vanificato dalla diminuzione del cerchio di massima confusione: su un formato più piccolo anche questo cerchio diviene più piccolo, così che si ha una conseguente diminuzione della profondità di campo (e un aumento del rumore, ma ne parleremo un’altra volta). Questa piccola diminuzione è però decisamente inferiore all’incremento dovuto alla corta lunghezza focale, così il bilancio complessivo è positivo. In conclusione si può affermare (grossolanamente ma tranquillamente) che la profondità di campo è dominata soprattutto dalla combinazione lunghezza focale – apertura del diaframma.
Per questo conviene parlare di “focale equivalenteï¿½ï¿½? usando le virgolette. L’unica equivalenza “veraï¿½ï¿½? è quella dell’angolo di copertura, la profondità di campo è diversa e per questa ragione i patiti dello sfocato selettivo non possono trovare soddisfazione nelle compatte.
Per la cronaca, questo è anche uno dei motivi per cui le compatte non hanno diaframmi che possano “chiudereï¿½ï¿½? più di tanto: non servono ad aumentare una profondità di campo già molto estesa, mentre causano facilmente fenomeni di diffrazione con le piccolissime celle del sensore.

Quanto detto finora si applica alla fotografia in generale.

Ma noi siamo subacquei e dobbiamo purtroppo fare i conti anche con fenomeni ottici peculiari dell’ambiente sommerso.
Un fenomeno in particolare ci interessa in questo caso: la rifrazione. Come ci insegna la legge di Snell, un raggio luminoso, attraversando due mezzi di diversa densità viene parzialmente rifratto: si allontanerà dalla normale all’interfaccia se passa da un mezzo più denso a uno meno denso, vi si avvicinerà nel caso contrario, da un mezzo meno denso a uno più denso.
L’aria è un mezzo meno denso dell’acqua e l’indice di rifrazione dell’acqua è di circa 1.33.
Tutti noi conosciamo perfettamente il fenomeno della rifrazione, per il quale abbiamo quell’effetto di avvicinamento e di ingrandimento dei soggetti che osserviamo quando siamo sott’acqua con la maschera: tutto ci appare più grande e vicino.

La rifrazione fa si che anche i nostri obiettivi cambino “lunghezzaï¿½ï¿½? e che si modifichi l’angolo di campo, nello specifico riducendosi di circa il 25%.

Quindi il mio obiettivo “normaleï¿½ï¿½?, il 50 mm, quando scafandrato e portato sott’acqua diventa un 70 mm, o meglio, ha l’angolo di campo di un 70 mm.
Questa è una legge fisica, che agisce sempre quando un raggio di luce attraversa mezzi a diversa densità e, con scarsissima sensibilità nei nostri confronti, se ne infischia delle tecnologie umane e di tutti i nostri problemi di fotografi subacquei.
Nel caso di utilizzo di reflex digitale scafandrata, questo ci pone naturalmente un ulteriore problema, da aggiungere al fattore di moltiplicazione digitale.
Dovremo infatti tenere conto, in aggiunta alla diminuzione di angolo di campo dovuta alle dimensioni del sensore, anche della riduzione della copertura dovuta alla rifrazione.

Vediamo un paio di tabelle. La prima riporta gli angoli coperti da diversi obiettivi, su sensore da 35 mm, in aria ed acqua:

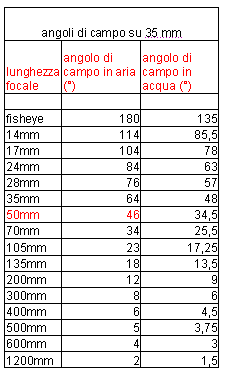
Nella seconda tabella sono riportati gli angoli di copertura delle diverse lunghezze focali, su 35 mm, su un sensore 1,8ï¿½ï¿½? e sullo stesso sensore ma in acqua.

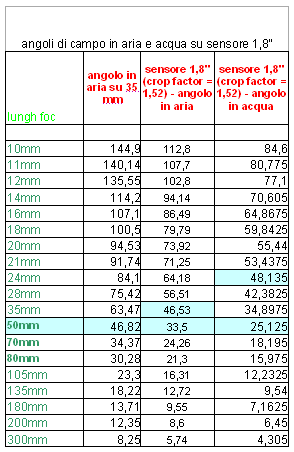
(ho riportato i calcoli su un sensore con un crop factor abbastanza diffuso; sulla stessa base ciascuno può fare i conti sul sensore in proprio possesso).

Come si può facilmente vedere, per avere la copertura di un 50 mm su questo sensore e sott’acqua dovrei montare un 24 mm, obiettivo che può a buona ragione essere definito un wide angle e non certamente un “normaleï¿½ï¿½?!

Utilizzando le nostre vecchie reflex a pellicola ci siamo abituati a gestire questa riduzione “a occhioï¿½ï¿½?, l’abbiamo per così dire interiorizzata e non ci turba più di tanto.
Sappiamo anche che per avere buone coperture con i grandangoli, e non perdere quel 25% di angolo di campo possiamo utilizzare un oblò sferico, che restituisce alla focale la sua originaria copertura, oltre a ridurre alcune aberrazioni geometriche dovute all’utilizzo di grandangoli e alla rifrazione.
Se siamo passati alla reflex digitale conservando il vecchio equipaggiamento di obiettivi e oblò, la rifrazione non ci spaventerà, la gestiremo come sempre tenendo conto esclusivamente del fattore di crop digitale.
Diverso è il discorso se invece parliamo di obiettivi a lunga focale, medi tele o tele. In questo caso la diminuzione di angolo di campo dovuta alla rifrazione va aggiunta effettivamente a quella dovuta al crop digitale, in quanto difficilmente useremo oblò sferici per tali obiettivi (francamente non so nemmeno se siano in vendita). Allora, come si vede dalla tabella, un bel 105 mm, che utilizzato su un sensore 1,8ï¿½ï¿½? già diminuisce il suo angolo di campo sino a corrispondere circa a un 135/140 mm, portato sott’acqua equivale addirittura a un 200!

Qualcuno mi ha fatto notare che tutto questo discorso potrebbe essere definito, per dirla con il mio professore di logica, “una sega mentaleï¿½ï¿½?. Forse è vero, se ragioniamo in termini di attrezzatura in nostro possesso.
Forse lo è di meno se invece stiamo valutando l’acquisto di nuova attrezzatura.
Allora ci sarà sicuramente utile, per orientarci nella scelta, considerare la misura del sensore della macchina prescelta non solo in termini di megapixel effettivi e di tecnologia, ma anche in termini di moltiplicatore di focale, e tenere altresì conto, nella scelta delle ottiche da portare sott’acqua e relativi accessori, anche della “antipaticaï¿½ï¿½? legge di Snell.

Insomma, come mi ha detto un amico: “se l’acqua produce l’ignobile effetto che dici, allora devi calcolarloï¿½ï¿½?.

Desidero a questo punto ringraziare Frank Tagliaferro, un fotografo e amico, per l’enorme e preciso lavoro di revisione e di controllo dei dati, oltre che per i preziosi consigli e informazioni e per le piacevolissime chiacchierate, dalle quali ho sempre tantissimo da imparare.

Bibliografia:
– “La fotografia digitale – come è fatta e come funzionaï¿½ï¿½? Ron White Ed. Mondatori Informatica
– “Lunghezza focale, angolo di campo e prospettivaï¿½ï¿½? Emanuele A. “Juzaï¿½ï¿½? su www.photorevolt.com
– www.dpreview.com
– Wikipedia

E’ assolutamente vietata la riproduzione, anche parziale, del testo e delle foto presenti in questo articolo, senza il consenso dell’autore.